基医期末复习
孩子们我回来了
前面几周一直在写ClaranCloudDisk,现在打算先停住寒假再写
不好孩子们,下周一就要考基医了孩子们,再不复习就要炸缸了
风好大,好凉快,大地在上升

孩子们,一起来复习基医吧
Pre
基础:高中生物知识 –> 非常重要,不然医学学着学着还要恶补高中知识
Main
绪论
冠状面/额状面/冠状轴:将人体分为前后的面/轴
矢状面/矢状轴:将人体分为左右的面/轴
水平面/垂直轴:请输入文本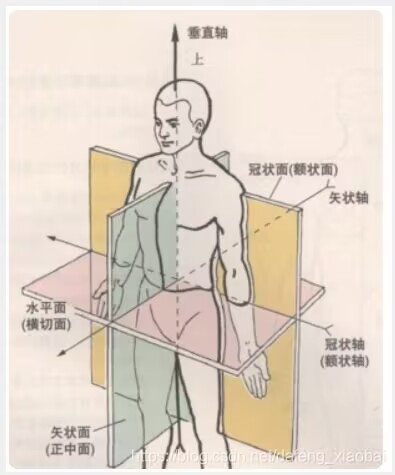
入体最主要调节方式:神经调节
神经调节的基本调节方式:反射 (详情见高中生物)
急性离体实验:急性指短时,离体rt,常见例子为神经不应期的测定
激素分泌:
- 远距分泌:血液运输
- 旁分泌:外液扩散
- 自分泌:rt,如肿瘤细胞
- 神经分泌:请输入文本
- (非激素传递方式)突触分泌:神经递质
解剖学姿势:身体直立,面向前方,双眼平视,两足并拢,足尖向前,双上肢下垂于躯干两侧,手掌向前
孩子们,周一我就复习了这么一点,我真是fvv😭😭😭mmM
孩子们我回来了,现在是2026.1.4-22:27,主包才发现电脑忘带电源适配器了
今天拼尽全力复习一天,终于战胜6个章节,还剩7个章节怎么办😭😭😭
第一章
随意肌/骨骼肌/横纹肌:能通过意识主动控制的肌肉
原发性主动转运:直接消耗atp
继发性主动转运:简介消耗atp,利用其他物质的顺浓度梯度差转运,可逆浓度转运
易化扩散:不可逆浓度
结缔组织:包括喜报,纤维和基质,继续包括骨组织,软骨组织,脂肪组织,血液,韧带等
结缔组织的特点:
- 细胞间质多,由细丝状的纤维、基质组成
- 细胞数量少,但种类多,无极性
上皮组织的特点:
- 成分多,间质少
- 有记性,分游离面和基底面
- 无血管、神经末梢丰富
- 有基膜
第四章
动作电位:“全或无”,短暂,可逆,可扩步
去极化:-70mV -> -50mV
超级化:-70mV -> -90mV
兴奋:去极化(超常期) -> 复极化 -> 超级化(低常期) -> 恢复
郎飞结:有髓神经末梢轴突外未被髓鞘包裹的区域,信号在郎飞结间跳跃传递,因此传导速度更快,离子跨膜移动总数更低,耗能更低,不衰减扩步
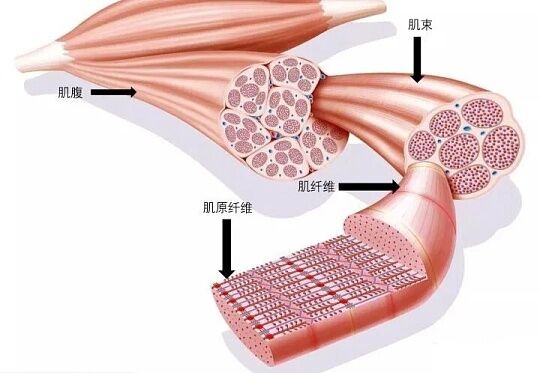
肌小节:肌肉基本单位
- 暗带(A带):由粗肌丝(含肌球蛋白)和细肌丝(部分)组成
- 明带(I带):有细肌丝(含肌动蛋白)组成
- H区:A带中的一部分。仅由粗肌丝再一次
- Z线:分隔肌小节的单位
- M线:H区中央固定粗肌丝的结构

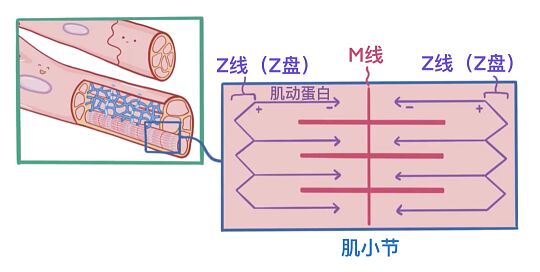
(✨重点!)滑行学说:
肌肉收缩时,细肌丝向肌小节中央M线方向滑行,使肌小节缩短
在这之中,只有细肌丝移动,粗肌丝不移动,细肌丝向M先移动,因此明带缩短,暗带不变
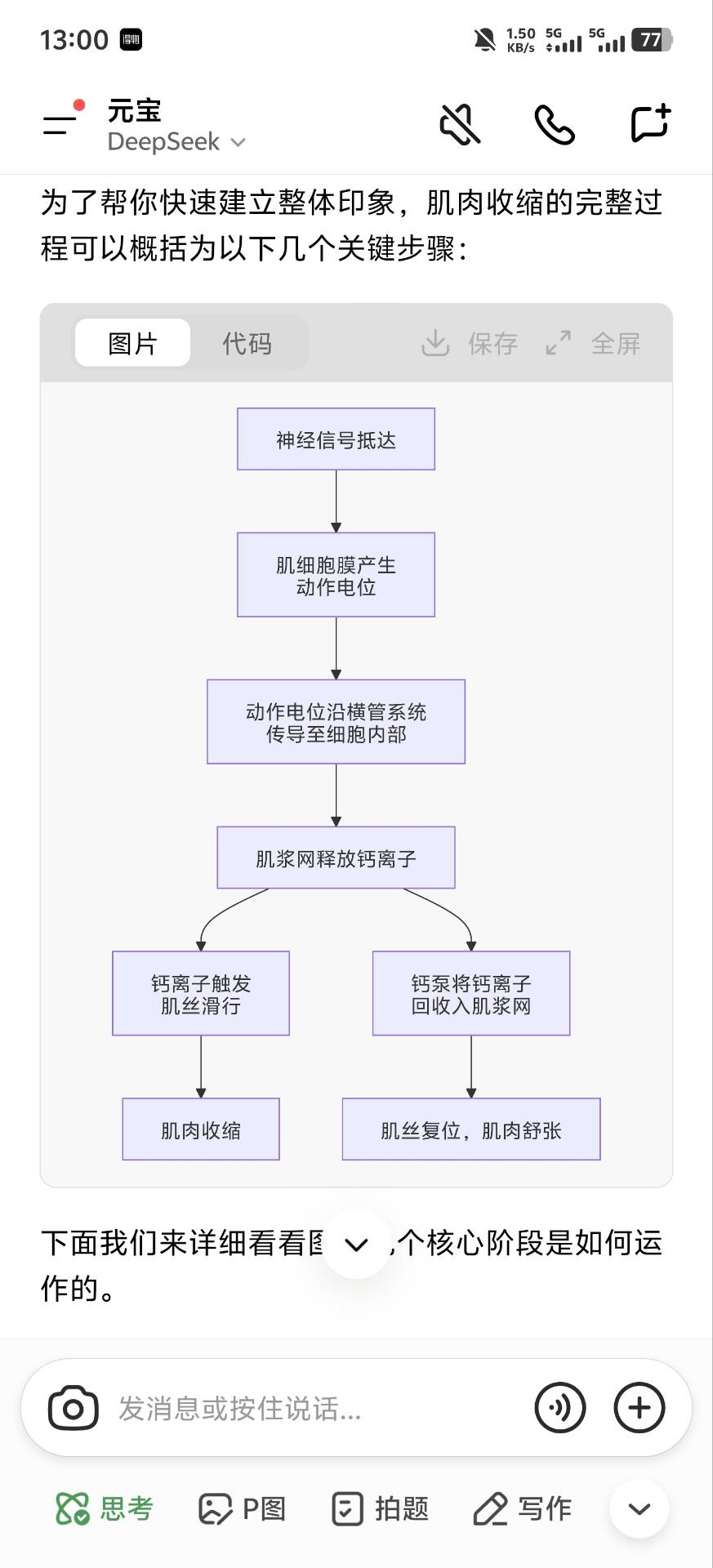
横管:肌膜上凹进去的部分,负责信号更深层次的传递
纵管:肌浆网,类内质网的膜系统,负责存储的调节钙离子浓度
终末池:纵管衍生膨大的部分
✨三联管:
由 终末池+横管+终末池 组成
横桥:肌球蛋白上可以与肌动蛋白位点结合,并拉动细肌丝与“横桥周期”的结构,多次重复上述过程可以形成肌肉滑动收缩
肌肉收缩的终极原理: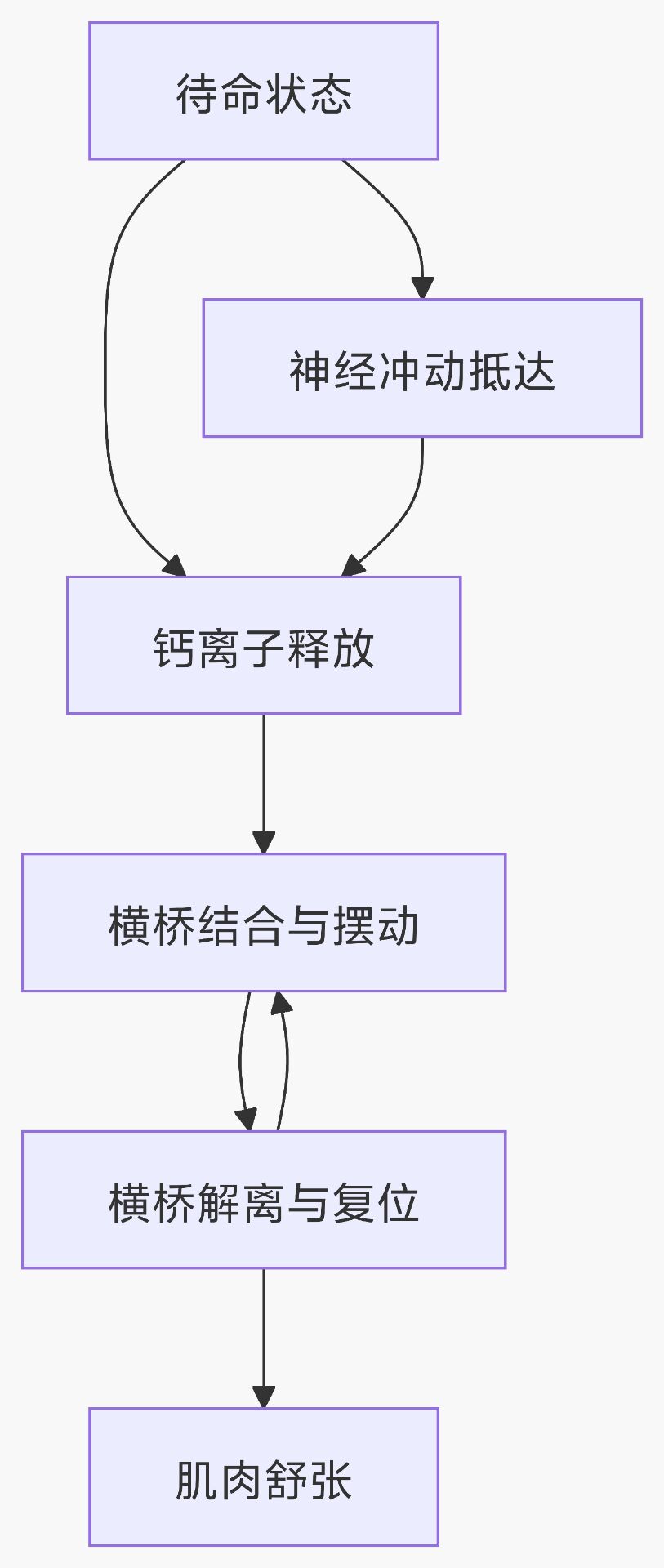

抗重力肌群:如图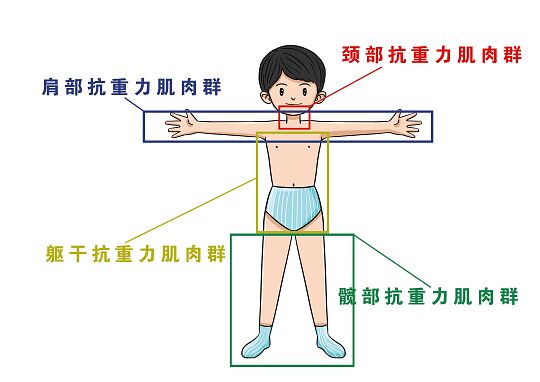
锥体系:如图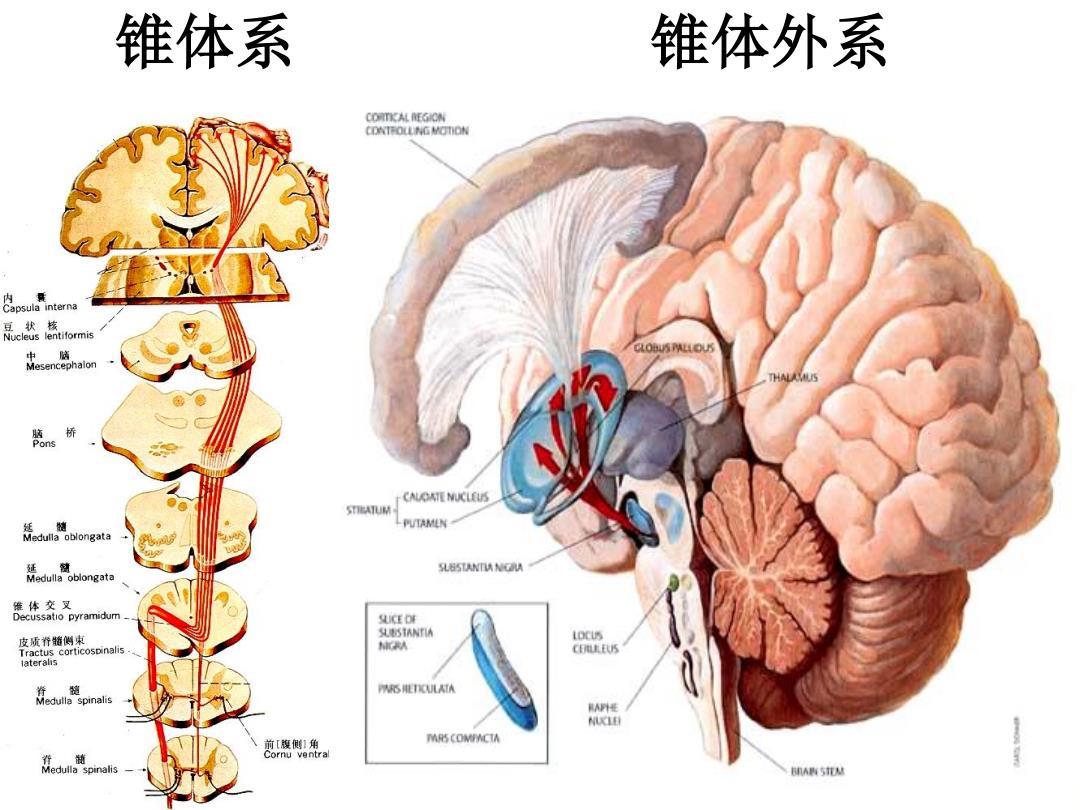
Ach:乙酰胆碱
第五章:神经系统
脊髓:中心有纵行的中央管,中央管的周围是灰质,白质位于脊髓的周围部分
神经核:中枢神经系统中相似的神经元包体和树突集中为灰质团块的结构
神经节:与神经核的区别为属于“周围神经系统”
EPSP:兴奋性突触后电位:突触间兴奋效果
IPSP:抑制性突触后电位:抑制效果
特异性投射系统&非特异性投射系统:精准投射(或不精准泛射)于大脑皮层以造成精确操作的
脑干:
- 延髓:心血管运动中枢+呼吸中枢
- 脑桥:链接上鞋+睡眠调节
- 中脑:视觉和听觉反射的初级中枢
脊休克:请输入文本,脊髓与高位中枢断离,肌张力下降或消失,血管扩张,血压下降,反射消失等,会慢慢恢复
第一信号:具体事务
第二信号:抽象事物,人类特征,如文字等
神经元联系方式:
- 环状式联系:一个神经元通过中间神经元,最终由返回自我影响的活动,用于后发放和反馈调节
- 单线式联系:链表
- 辐散式联系:一对多
- 聚合式联系:多对一,总和的结构基础
几茶酚胺类:多巴胺,贤上腺素,去甲肾上腺素
在感神经节后纤维的递质是:Ach
小脑:
- 绒球小结叶:调节身体平衡
- 小脑前叶:调节肌张力
- 小脑后叶:随意运动
间脑:
- 背侧丘脑:皮质下高级感觉中枢
- 下丘脑:内脏活动和内分泌&情绪调节中枢
以下属于胆碱能受体的是:M,N1,N2
脊髓&神经:
- 本体感觉和精细触觉通路:同侧,上行
- 痛觉与温度觉通路:对侧,交叉,上行
- 随意运动通路:对侧,交叉,下行
用于解决脊髓半截断相关题目
α-运动神经元:支配梭外肌纤维
γ-运动神经元:支配梭内肌纤维
Spec:
- 支配肾上腺髓质的交感神经不需要换元
- 绝大部分交感神经的节后纤维属于肾上腺素神经
视觉皮层代表区位于:枕叶距状裂(wtf?)
大脑皮层投射区:
- 中央前回:初级运动
- 中央后回:躯体感觉
- 枕叶皮层:视觉
- 皮层边缘:边缘系统:情绪,记忆,内脏…
腱器官抑制肌梭
肌梭引起牵张反射
游离神经末梢:痛觉
认得基本生命中枢位于:延髓
摄食中枢位于:丘脑
简述感觉传导通路:
脊神经节 –(脊髓)– 延髓 – 内侧丘系 –(对侧)– 丘脑 – 大脑皮层
第六章:感觉系统
请输入文本,最简单的一集
懒得写了,直接拍笔记吧
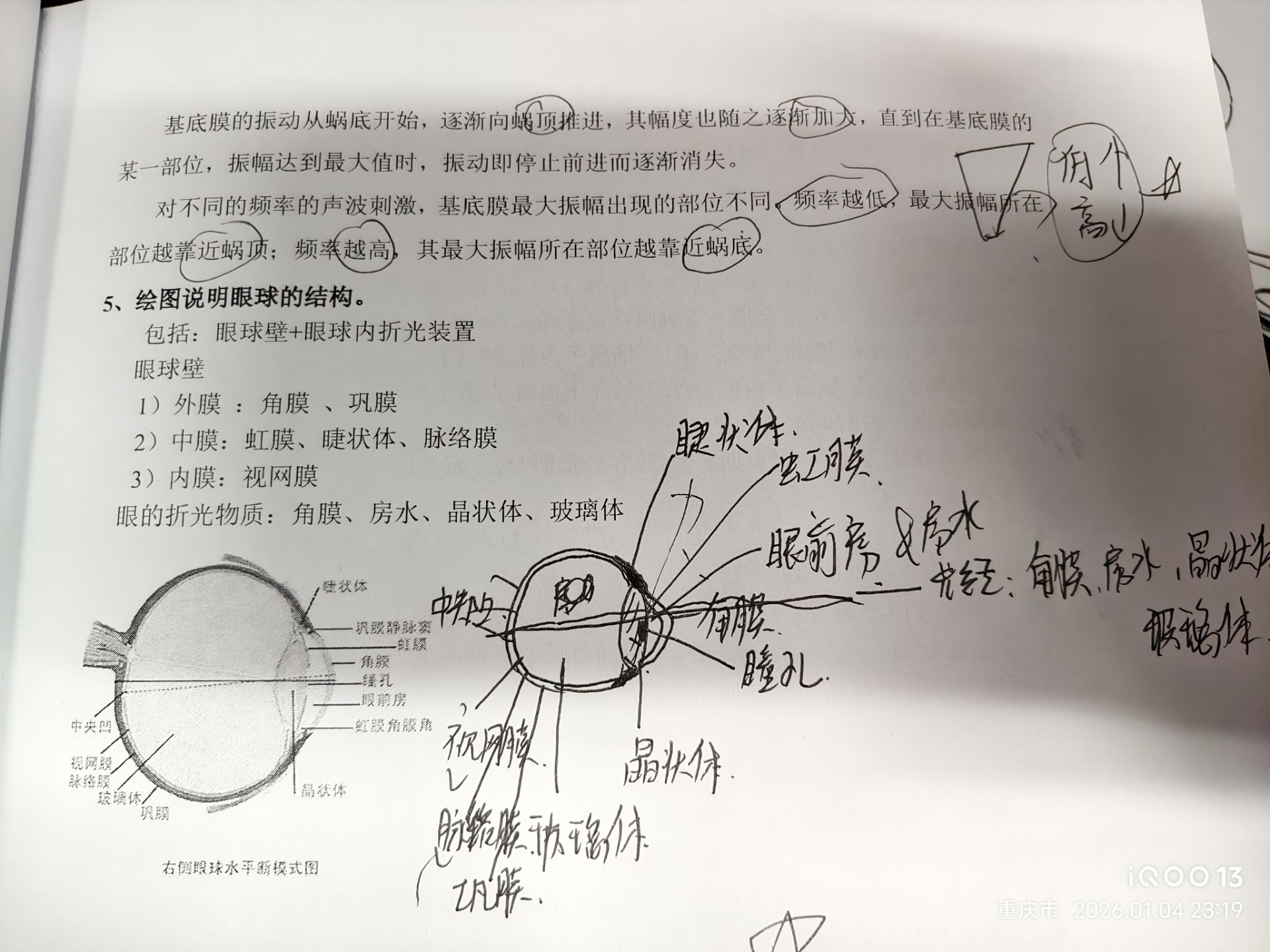
第九章:循环系统
最难的一集


孩子们,我还没复习完,只复习到这里😭😭😭
还有4章😭😭😭
我去了孩子们,我的资料是老版本的,又多了3章没复习😭😭😭
怎么办孩子们😭😭😭明天下午一点考试😭😭😭现在是晚上十一点半😭😭😭
明早起来在草草地看两章吧😭😭😭给他就是了😭😭😭
其他
孩子们我看完了(其实还有两章没看)!
但是没时间归档到blog上了,不搞了!
End
哈哈哈哈哈孩子们我考完了!太几把简单了哈哈哈!感谢老师!!!
挂科已然成为不可能之事!!!
