高数期中复习

发表于 2025-11-30 分类于杂项阅读次数：

Re：从零开始的高数学习笔记

无穷小的分类和等价无穷小的替换

无穷小的分类

$无穷小1.jpg$

高阶无穷小 – 0
低阶无穷小 – 无穷
同阶无穷小 – C
等价无穷小 – 1

等价无穷小

$无穷小2.jpg$

重点公式！！！

$无穷小3.jpg$
$无穷小4.jpg$

等价无穷小的替换

$替换1.jpg$

例题和注意事项

$替换2.jpg$
$替换3.jpg$
$替换4.jpg$

函数的间断和连续

连续

定理

$连续1.jpg$

左右连续

$连续2.jpg$

示例

$连续3.jpg$

区间连续

$连续4.jpg$

间断

无穷/震荡/跳跃/可去间断点

$间断1.jpg$
$间断2.jpg$
$间断3.jpg$

第一、二类间断点

$间断4.jpg$
$间断5.jpg$

例题

$间断6.jpg$

闭合函数的连续性

定理

$连续性1.png$

例题

$连续性2.png$
$连续性3.png$
$连续性4.png$
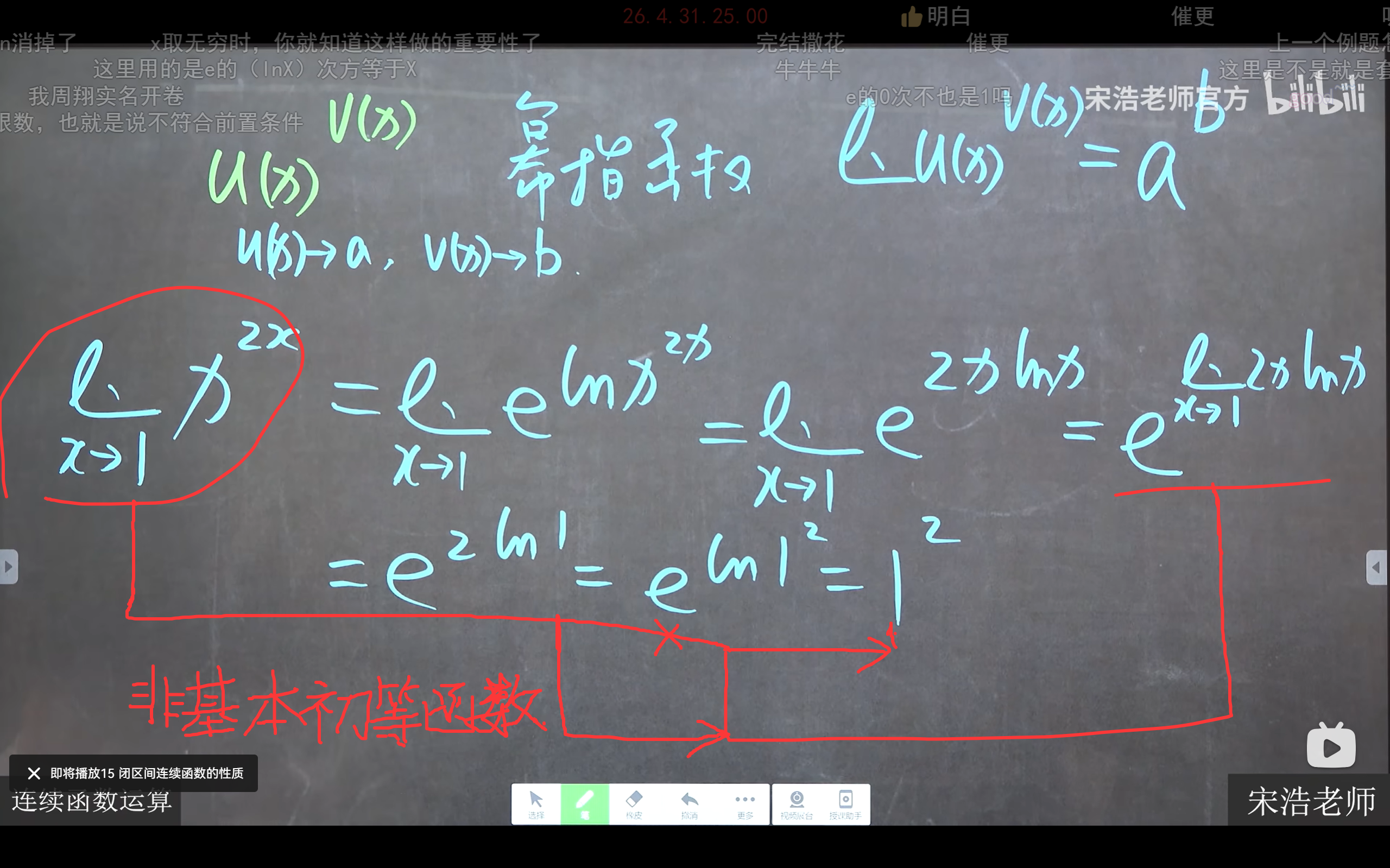
$连续性5.png$

最大值与最小值的定义

$maxmin.png$

零点存在定理

$连续性6.png$

导数

导数定义

左右导数

$导数.png$

导数定理

$导数1.png$

反函数的求导

法则

$反函数1.png$

例题

$反函数2.png$

公式

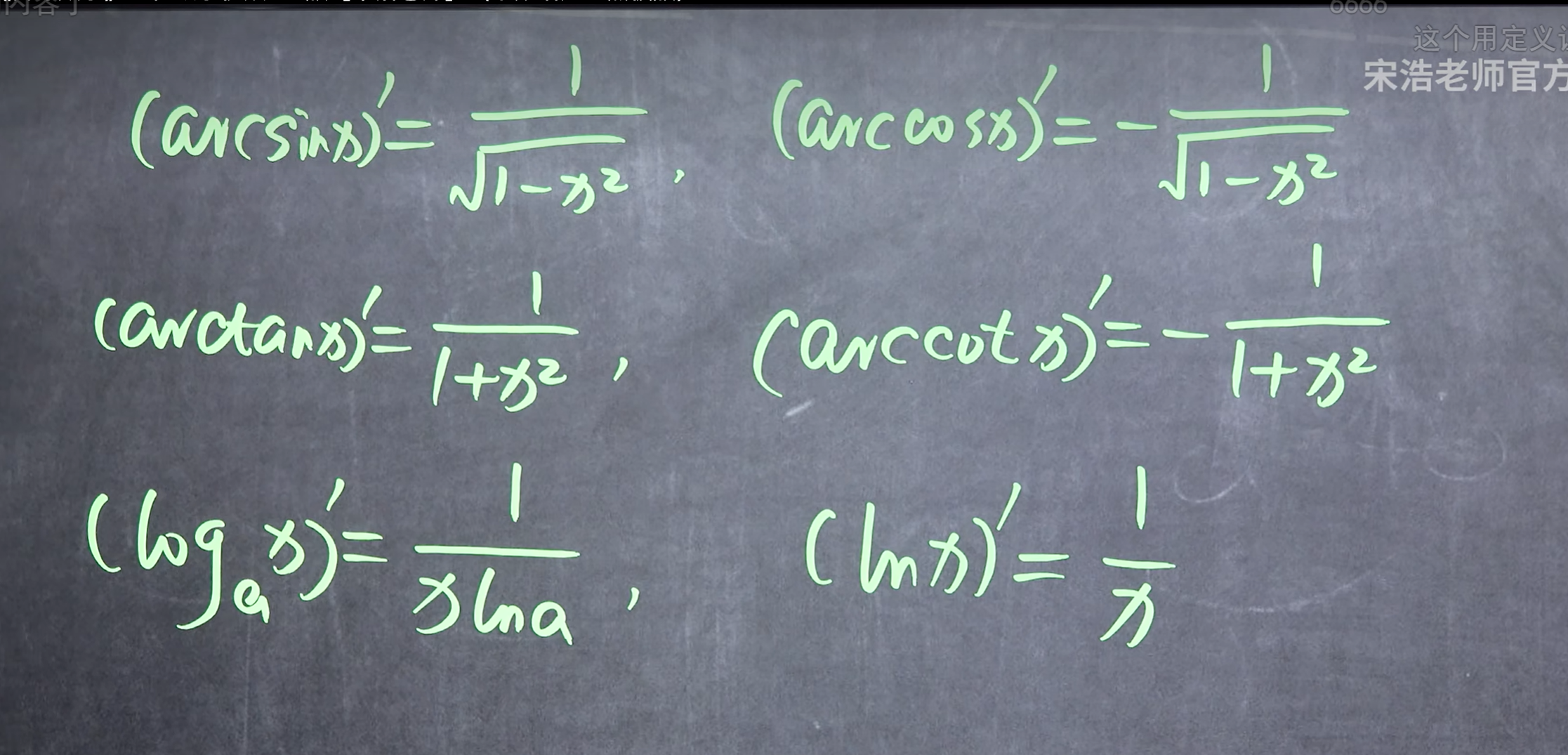
$反函数3.png$

复合函数的求导

$复合.png$

三角函数求导公式

$三角.png$

高阶导数

定理

$高阶导1.png$

公式

$高阶导2.png$

例题

$高阶导3.png$

莱布尼茨定理

$高阶导4.png$

隐函数求导

方法

$隐函数1.png$

例题

$隐函数2.png$

二阶导例题

$隐函数3.png$

对数求导法

对于无法直接求导的函数，先同时取对，再用隐函数求导法解决
$隐函数4.png$
或者对函数右边进行同构，起到一样的效果
$隐函数5.png$
也可用于较为复杂的只包含二三级运算的函数
$隐函数6.png$

参数方程求导

定理

$参数1.png$

二阶导

$参数2.png$

例题

$参数3.png$

微分

微分的定义

$微分1.png$
$微分2.png$
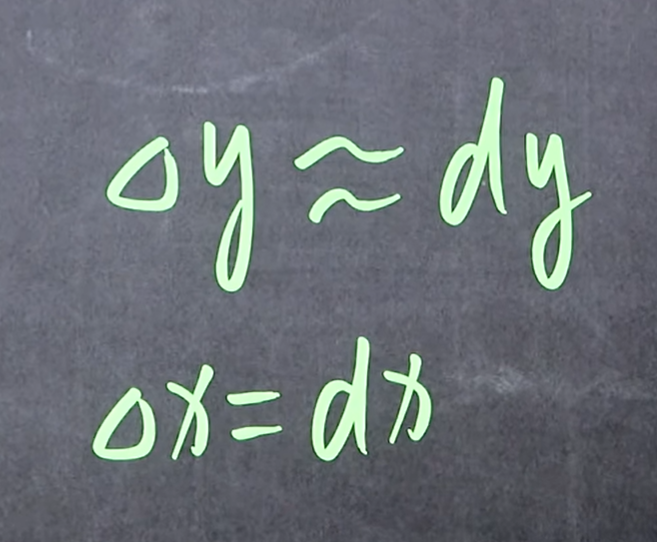
$微分3.png$

公式

A=f’(x)
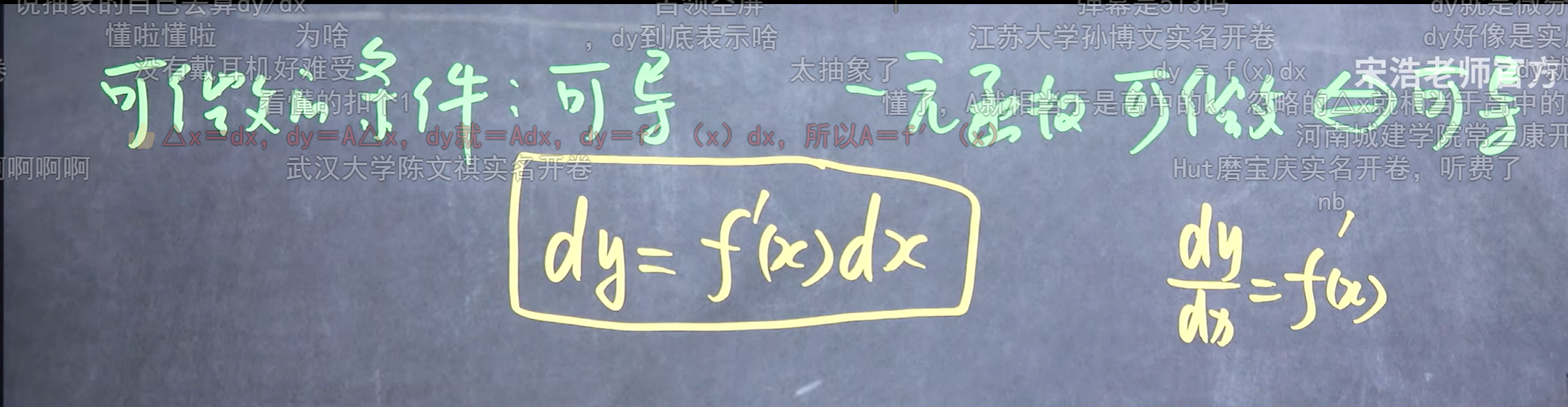
$微分4.png$
$微分5.png$

例题和几何含义

$微分6.png$

复合函数的微分法则

本质上就是复合函数的求导+dx
$微分7.png$

近似计算

定义

$近似计算1.png$

例题

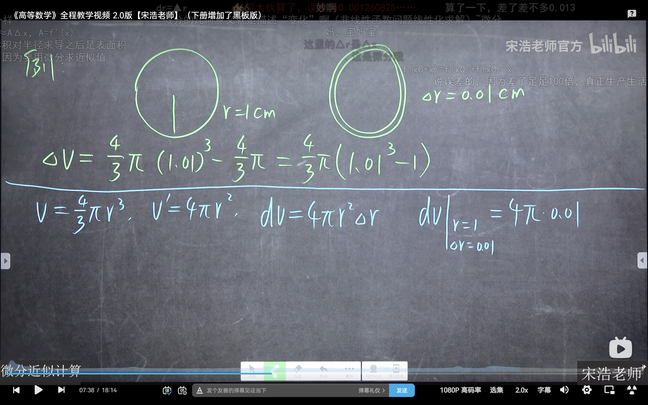
$近似计算2.png$
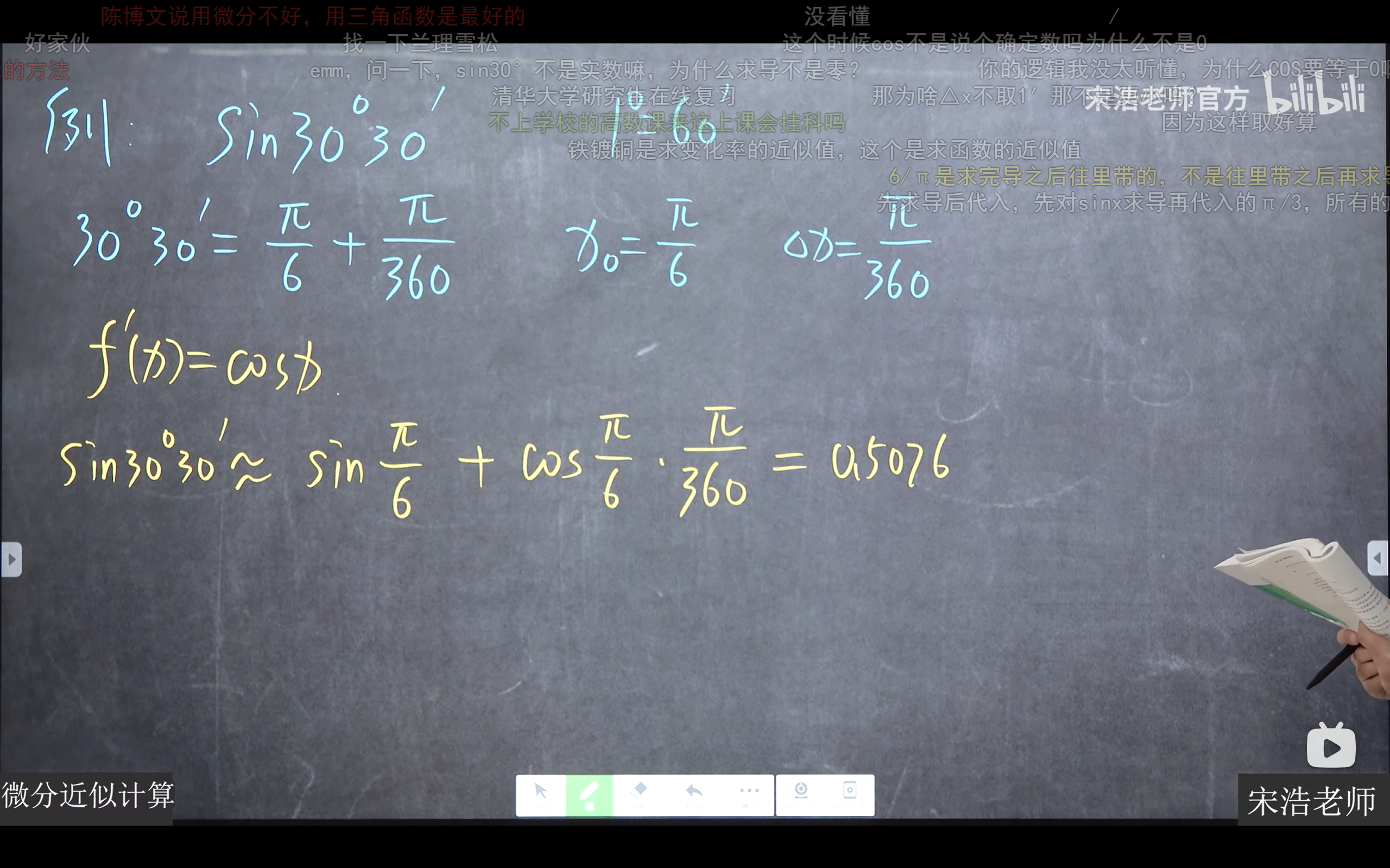
$近似计算3.png$

应用

与等价无穷小类似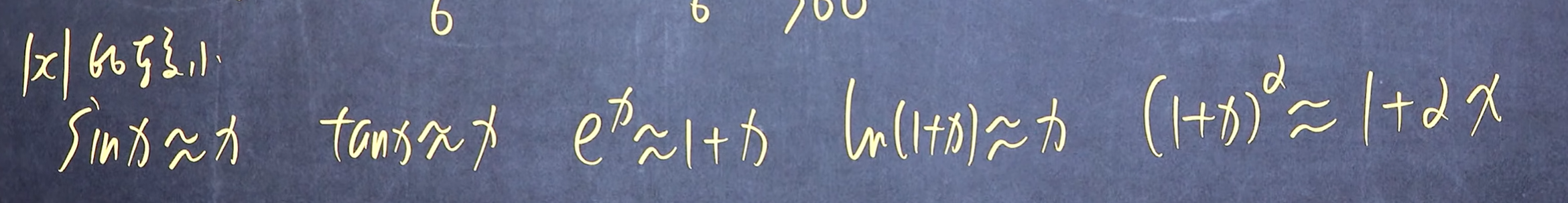
$近似计算34png.png$

中值定理

费马引理

$费马.png$

罗尔定理

$罗尔.png$

拉格朗日中值定理

$拉格朗日.png$

引申

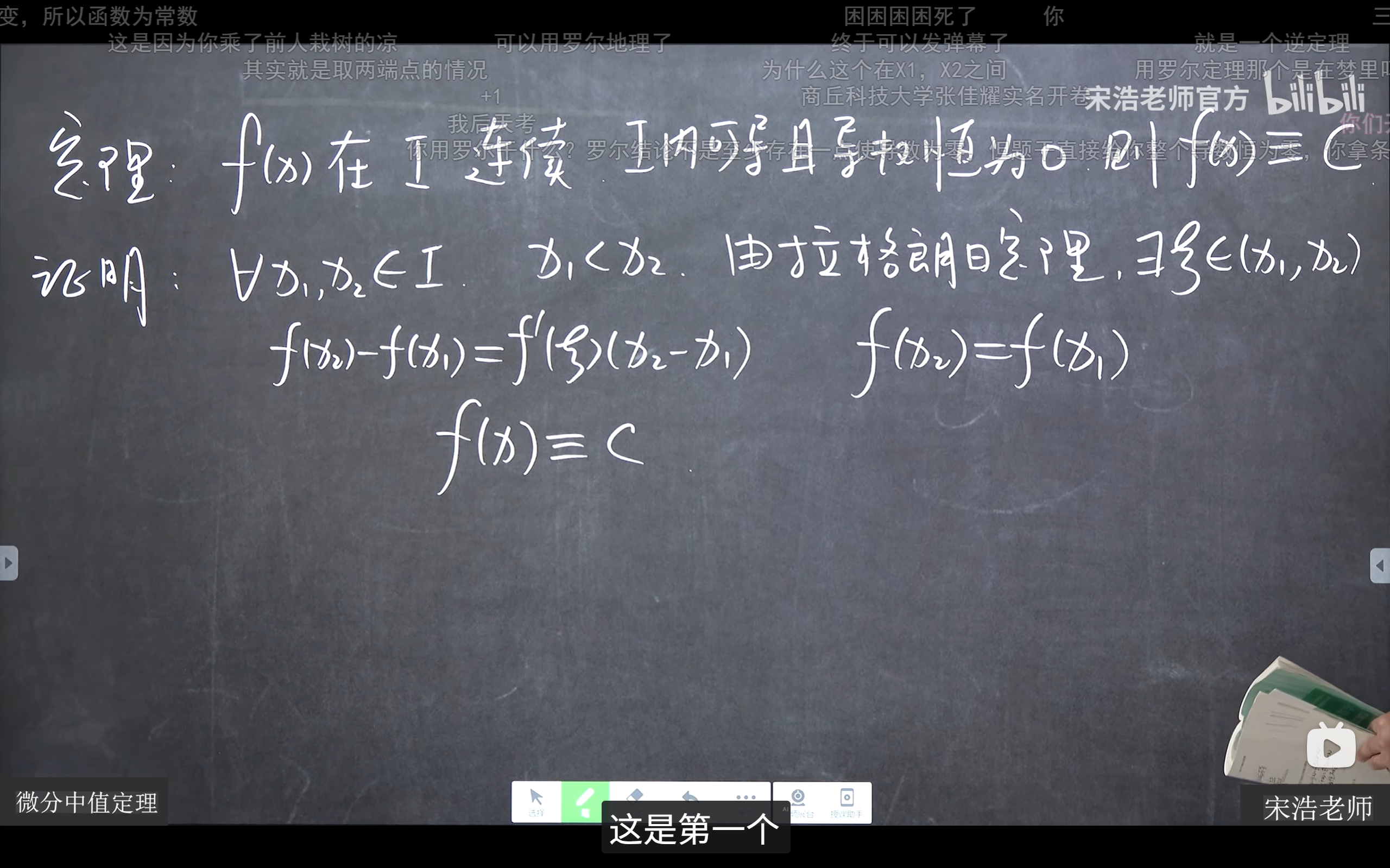
$拉格朗日1.png$

例题

$拉格朗日2.png$

柯西中值定理

本质上是将x和y变为了两个参数方程
$Cauthy.png$
$Cauthy1.png$

洛必达

定理

$洛必达1.jpg$

示例

$洛必达2.jpg$
$洛必达3.jpg$

注意事项

$洛必达4.jpg$

变式

$洛必达5.jpg$

例题

$洛必达例题1.jpg$
$洛必达例题2.jpg$
$洛必达例题3.jpg$
$洛必达例题4.jpg$

0%